Distribuciones Continuas
DISTRIBUCIÓN JI-CUADRADA (X2)
En realidad la distribución ji-cuadrada es la distribución
muestral de s2. O sea que si se extraen todas las muestras posibles
de una población normal y a cada muestra se le calcula su varianza, se obtendrá
la distribución muestral de varianzas.
Para estimar la varianza
poblacional o
la desviación estándar, se necesita conocer el estadístico X2. Si se
elige una muestra de tamaño n de una población normal con varianza
, el estadístico:
tiene una distribución muestral que es una distribución ji-cuadrada con gl=n-1 grados de libertad y se denota X2 (X es la minúscula de la letra griega ji). El estadístico ji-cuadrada esta dado por:
, el estadístico:
tiene una distribución muestral que es una distribución ji-cuadrada con gl=n-1 grados de libertad y se denota X2 (X es la minúscula de la letra griega ji). El estadístico ji-cuadrada esta dado por:
donde n es el tamaño de la muestra, s2 la varianza muestral
y la varianza de la población de donde se
extrajo la muestra. El estadístico ji-cuadrada también se puede dar con la
siguiente expresión:
Propiedades de las distribuciones ji-cuadrada
1. Los valores de X2 son
mayores o iguales que 0.
2. La forma de una distribución X2 depende
del gl=n-1. En consecuencia, hay un número infinito de distribuciones X2.
3. El área bajo una curva ji-cuadrada y sobre
el eje horizontal es 1.
4. Las distribuciones X2 no son
simétricas. Tienen colas estrechas que se extienden a la derecha; esto es,
están sesgadas a la derecha.
5. Cuando n>2, la media de una distribución
X2 es n-1 y la varianza es 2(n-1).
6. El valor modal de una distribución X2 se
da en el valor (n-3).
La siguiente figura ilustra tres distribuciones X2. Note que el
valor modal aparece en el valor (n-3) = (gl-2).
para x>0
La tabla que se
utilizará para estos apuntes es la del libro de probabilidad y estadística de
Walpole, la cual da valores críticos  (gl) para veinte valores especiales de
(gl) para veinte valores especiales de  . Para denotar el valor crítico de una distribución X 2 con
gl grados de libertad se usa el símbolo (gl); este valor crítico
determina a su derecha un área de bajo la curva X2 y sobre el
eje horizontal. Por ejemplo para encontrar X20.05(6) en
la tabla se localiza 6 gl en el lado izquierdo y
. Para denotar el valor crítico de una distribución X 2 con
gl grados de libertad se usa el símbolo (gl); este valor crítico
determina a su derecha un área de bajo la curva X2 y sobre el
eje horizontal. Por ejemplo para encontrar X20.05(6) en
la tabla se localiza 6 gl en el lado izquierdo y  a o largo del lado superior de la misma tabla.
a o largo del lado superior de la misma tabla.
 (gl) para veinte valores especiales de
(gl) para veinte valores especiales de  . Para denotar el valor crítico de una distribución X 2 con
gl grados de libertad se usa el símbolo (gl); este valor crítico
determina a su derecha un área de bajo la curva X2 y sobre el
eje horizontal. Por ejemplo para encontrar X20.05(6) en
la tabla se localiza 6 gl en el lado izquierdo y
. Para denotar el valor crítico de una distribución X 2 con
gl grados de libertad se usa el símbolo (gl); este valor crítico
determina a su derecha un área de bajo la curva X2 y sobre el
eje horizontal. Por ejemplo para encontrar X20.05(6) en
la tabla se localiza 6 gl en el lado izquierdo y  a o largo del lado superior de la misma tabla.
a o largo del lado superior de la misma tabla.Cálculo de Probabilidad
El cálculo de
probabilidad en una distribución muestral de varianzas nos sirve para saber
como se va a comportar la varianza o desviación estándar en una muestra que
proviene de una distribución normal.
Ejemplos:
1.-Suponga que los
tiempos requeridos por un cierto autobús para alcanzar un de sus destinos en
una ciudad grande forman una distribución normal con una desviación
estándar  =1 minuto. Si se elige al azar una muestra de 17 tiempos, encuentre la
probabilidad de que la varianza muestral sea mayor que 2.
=1 minuto. Si se elige al azar una muestra de 17 tiempos, encuentre la
probabilidad de que la varianza muestral sea mayor que 2.
Solución:
El valor de 32 se
busca adentro de la tabla en el renglón de 16 grados de libertad y se encuentra
que a este valor le corresponde un área a la derecha de 0.01. En consecuencia,
el valor de la probabilidad es P(s2>2)
Estimación de la Varianza
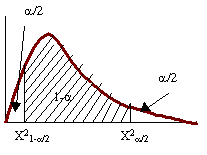
Los valores de X2 dependerán
de nivel de confianza que se quiera al cual le llamamos  . Si nos ubicamos en la gráfica se tiene:
. Si nos ubicamos en la gráfica se tiene:
 . Si nos ubicamos en la gráfica se tiene:
. Si nos ubicamos en la gráfica se tiene: La distribución Normal
El modelo de
distribución Normal es el más utilizado en Estadística, ya que:
a) Muchas
distribuciones de datos reales pueden ser representadas por la distribución
Normal.
b) Tiene
propiedades que la hacen especialmente útil.
c) Representa la
distribución de muchos de los acontecimientos que ocurren al azar.
En realidad, el nombre de Normal proviene
del hecho de que durante un tiempo se creyó, por parte de médicos y biólogos,
que todas las variables naturales de interés seguían este modelo.
que, como vemos,
depende de dos parámetros μ (que puede ser cualquier valor real) y σ (que
ha de ser positiva). Por esta razón, a partir de ahora indicaremos de forma
abreviada que una variable X sigue el modelo
Normal así: X ~ N(μ, σ). Por ejemplo, si nos
referimos a una distribución Normal con μ = 0 y
σ = 1 lo abreviaremos N(0, 1).
A continuación
presentamos la gráfica de esta función de densidad (donde se pueden cambiar los
parámetros):
Una distribución normal de media μ y desviación típica σ se designa porN(μ, σ). Su gráfica es la campana de Gauss:
El área del recinto determinado por
la función y el eje de abscisas es igual a la
unidad.
Al
ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5
a la izquierda y otra igual a 0.5 a la derecha.
La probabilidad equivale al área encerrada bajo la curva.
Propiedades del modelo Normal
1.
Su esperanza
es μ.
2.
Su
varianza es σ2 y, por tanto, su desviación típica es σ.
3.
Es
simétrica respecto a su media μ, como puede apreciarse en la representación
anterior.
4.
Media,
moda y mediana coinciden (μ).
5.
Cualquier
transformación lineal de una variable con distribución Normal seguirá también
el modelo Normal. Si X ~ N(μ, σ) y definimos Y = aX + b (con a ≠
0), entonces Y ~ N(aμ + b, |a|σ). Es decir, la esperanza de Y será aμ
+ b y su desviación típica, |a|σ.
6.
Cualquier
combinación lineal de variables normales independientes sigue
también una distribución Normal. Es decir, dadas n variables
aleatorias independientes con distribución Xi ~ N(μi,
σi) para i = 1, 2, ..., n la
combinación lineal: Y = anXn + an−1Xn−1+
... + a1X1 + a0 sigue
también el modelo Normal:
Distribución normal estándar
N(0, 1)
La distribución normal estándar, o tipificada o reducida, es
aquella que tiene por media el valor cero, μ =0,
y por desviación típica la unidad, σ =1.
La probabilidad de la variable X dependerá
del área del recinto sombreado en la figura.
Tipificación de la variable
Para poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).
La Distribución T de Student
En la generalidad de los casos, no disponemos de la
desviación standard de la población, sino de una estimación calculada a partir
de una muestra extraída de la misma y por lo tanto no podemos calcular Z.
En estos casos calculamos el estadístico T:
T=μ−xs
con
donde S es la desviación standard muestral, calculada con
n-1 grados de libertad.
Utilizamos S, la Desviación Standard de una
Muestra, en lugar de μ, la Desviación Standard de la Población.
El estadístico T tiene una distribución que se denomina
distribución T de Student, que está tabulada para 1, 2, 3, ... etc. grados de
libertad de la muestra con la cual se calculó la desviación standard. La
distribución T tiene en cuenta la incertidumbre en la estimación de la
desviación standard de la población, porque en realidad la tabla de T contiene
las distribuciones de probabilidades para distintos grados de libertad.
La distribución T es mas ancha que la distribución normal
tipificada Para un número de grados de libertad pequeño. Cuando los grados de
libertad tienden a infinito, la distribución T tiende a coincidir con la
distribución normal standard. Es decir, en la medida que aumentemos el número
de observaciones de la muestra, la desviación standard calculada estará mas
próxima a la desviación standard de la población y entonces la distribución T
correspondiente se acerca a la distribución normal standard. El uso de la
distribución T presupone que la población con que estamos trabajando tiene una
distribución normal.
La distribución t es útil para realizar inferencias acerca de la media poblacional cuando no se conoce s y la población es normal, independiente del n, no obstante, aún cuando la distribución sea un tanto sesgada, la t sigue siendo apropiada, esto se conoce como una distribución robusta, es decir, a cambios moderados de los supuestos, el modelo sigue siendo valido. Como en el caso de la distribución normal, ésta distribución también usa valores tabulados, tal como se aprecian en la tabla precedente, teniendo en cuenta, que a medida que los g.l aumenten los valores tienden a ser igual a los encontrados en la tabla Z.
Ejemplo
P(μ<20.5)
Estandarizamos T=(X-μ)/(s/√n) que sigue una distribución t de n-1 grados de libertad
T=(20.5-20)/(1/√25) = 2.5
P(μ<20.5) --> P(T<2.5) ~ t(24)
P(T<2.5) = 0.9902
P(μ<20.5)=0.9902
La probabilidad que la longitud media de la muestra de 25 tornillos sea inferior a 20.5 mm es del 99.02%
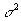













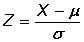



0 comentarios:
Publicar un comentario
Suscribirse a Enviar comentarios [Atom]
<< Inicio